Activité : Equilibre théorique de Hardy Weinberg
Introduction :
Les recherches sur l’évolution des espèces se séparent en deux volets : les unes visent la reconstruction de l’histoire de la vie, les autres tendent à comprendre les modalités et les processus de l’évolution. Ici nous allons chercher à comprendre les processus évolutifs.
En 1908, Godfrey Harold Hardy et Wilhem Weinberg ont voulu appliquer la génétique mendellienne pour comprendre l’évolution des génotypes au sein d’une population au cours des générations. Indépendamment, ils ont établi la même loi appelée équilibre de Hardy-Weinberg.
Une population est un ensemble d’individus de la même espèces vivant dans une même zone, se reproduisant ensemble et formant une descendance fertile. Les individus de ces populations présentent des génomes identiques (mêmes gènes) car sont de la même espèce, mais des génotypes différents (allèles différents), donc des phénotypes différents.
Pour le généticien, une population est un ensemble de génotypes. La structure génétique d’une population est représentée par l’ensemble des allèles présents dans la population. La fréquence de ces allèles peut varier au cours du temps de façon plus ou moins importante.
Problème
Qu’est-ce que l’équilibre de Hardy-Weinberg ? Permet-il expliquer l’évolution des génotypes dans les populations?
Objectifs :
- Comprendre la formulation d’une loi mathématique
- Appliquer et interpréter un modèle sur des exemples concrets
Consigne :
On considère un caractère gouverné par un gène possédant 2 allèles A et a de fréquences p et q dans la génération 0 pour une espèce diploïde à reproduction sexuée.
Les fréquences des gamètes (A) et (a) sont donc égales aux fréquences alléliques p et q parmi les adultes de la population qui les ont produits.
Comme il n’y a que 2 allèles, p + q = 1.
- En réalisant un tableau de croisement des gamètes de cette population, déterminer la fréquence des génotypes dans la génération suivante (génération 1) :
| Croisement aléatoire au sein de la population | Gamète femelle (A) de fréquence p | Gamète femelle (a) de fréquence q |
| Gamète mâle (A) de fréquence p | ||
| Gamète mâle (a) de fréquence q |
Fréquence (A//A) =
Fréquence (A//a) =
Fréquence (a//a) =
- Sachant que la somme des fréquences de ces différents génotypes est = à 1 (ou 100%), écrire l’expression mathématique de l’équilibre théorique de Hardy-Weinberg en écrivant cette égalité :
- Calculer la fréquence allélique en génération 1
(Simplifier en ne laissant qu’une inconnue car p+q=1).
Fréquence de (A) = Freq(A//A) + ½ Freq(A//a) =
Fréquence de (a) = Freq(a//a) + ½ Freq(A//a) =
- Comparer les fréquences alléliques des génération 0 et 1. Quelle remarque peut-on faire en terme d’évolution dans les générations suivantes.
Appliquons cette loi à des exemples précis :
EXEMPLE 1 : Les globules rouges
Les globules rouges portent à leur surface des molécules qui peuvent être reconnues pas des anticorps. Les plus connues sont celles qui déterminent les groupes sanguins ABO. Il existe beaucoup d’autres molécules permettant d’établir des groupes sanguins, comme les molécules M et N. Elles sont codées par un gène possédants deux allèles M et N. Dans les années 1950, le génotype pour ce gène a été déterminé pour un échantillon de 1416 habitants d’une ville japonaise.
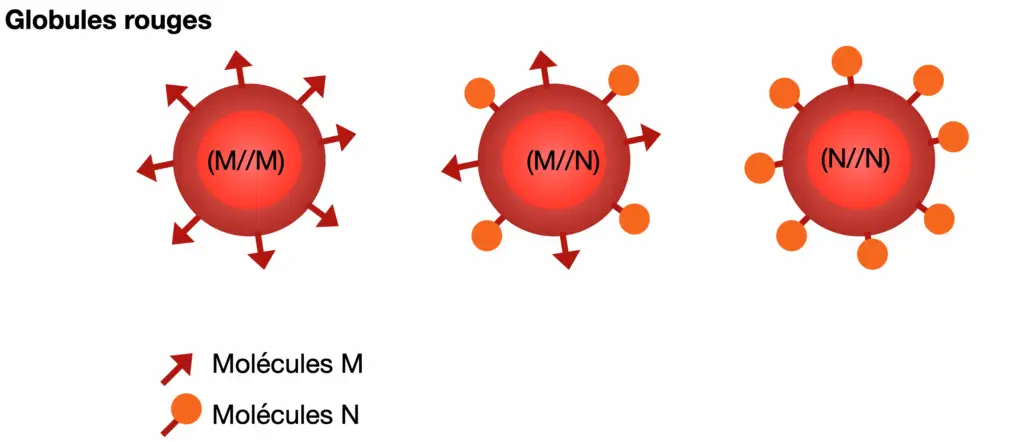
- Cacluler la fréquence observée des génotypes puis calculer les fréquences alléliques F(M) et F(N) dans la population et selon ces fréquences, les fréquences génotypiques théorique attendues selon le modèle de Hardy-Weinberg.
- Déterminer si la structure génétique de la population étudiée est en accord avec la loi de Hardy-Weinberg.
Aide : En partant des effectifs, la fréquence de (A) = Nombre de (A//A) + ½ Nombre de (A//a)
population totale
Génotypes | M//M (Groupe M) | M//N (Groupe MN) | N//N (Groupe N) |
| Nombre d’individus | 406 | 744 | 332 |
| Fréquence génotypique observée | |||
| Fréquence génotypique théorique |
Fréquence alléliques : F(M)= F(N)=
EXEMPLE 2 : Les loups de Yellowstone
La populations de loups du parc de Yellowstone présente deux couleur de fourrure : noire ou grise. La couleur de la fourrure est contrôlée par un gène qui existe sous deux allèles : N (dominant) sur n (récessif).

- Cacluler la fréquence observée des génotypes puis calculer les fréquences alléliques F(N) et F(n) dans la population et selon ces fréquences, les fréquences génotypiques théorique attendues selon le modèle de Hardy-Weinberg.
- Déterminer si la structure génétique de la population étudiée est en accord avec la loi de Hardy-Weinberg.
Génotypes | N//N Loups noirs | N//n Loups noirs | n//n Loups gris |
| Nombre d’individus | 31 | 321 | 413 |
| Fréquence génotypique observée | |||
| Fréquence génotypique théorique |
Fréquence alléliques : F(N)= F(n)=
- A l’aide des informations ci-dessous, trouver deux explications à l’écart constaté entre fréquences observées et fréquences théoriques des génotypes.
Génotypes | N//N Loups noirs | N//n Loups noirs | n//n Loups gris |
| Survie moyenne annuelle | 0.47 | 0.77 | 0.75 |
| Nombre moyen de petits | 0.031 | 2.35 | 1.83 |
EXEMPLE 3 : Les allèles neutres
Un allèle neutre est un allèle ne conférant au phénotype ni avantage, ni désavantage. Il apparaît comme tout allèle, par mutation, au hasard, dans la population.
Ici on regarde l’évolution (sur 100 générations) de la fréquence d’un allèle neutre dans 7 populations de 1000 individus (correspondants aux 7 courbes de couleurs) dont la fréquence initiale de l’allèle dans la génération 0 est p=0,5.
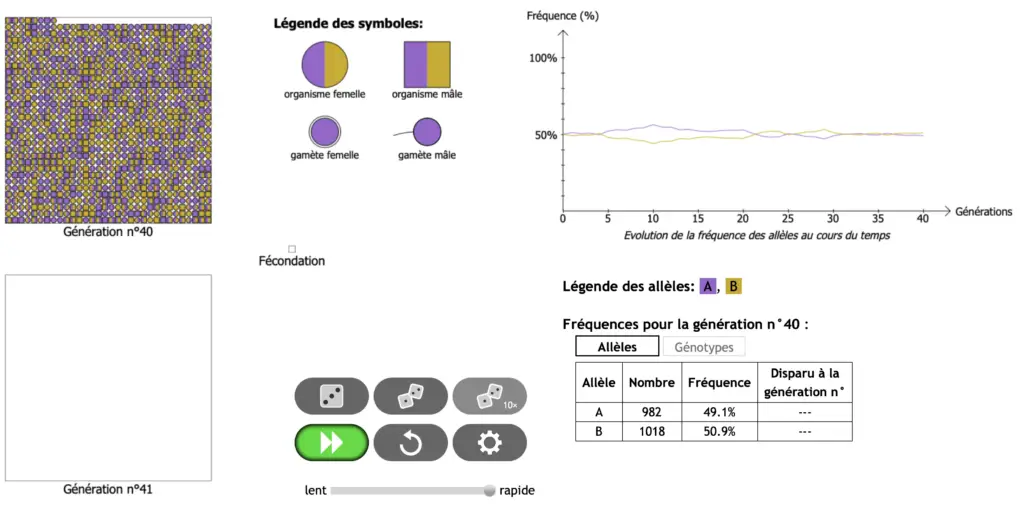
On fait la même observation pour 7 populations de 50 individus.
Petite activité de dérive des allèles
Protocole :
- Tester par vous-même la structure génétique des populations en fonction de leurs effectifs avec le logiciel : https://www.pedagogie.ac-nice.fr/svt/productions/derive-diplo/index.htm
Simulation
- Choisir 2 allèles avec fréquence du 1er allèle = 50% (soit 0.5) et un effectif de 1000. Autorisez les mutations à 10%. Valider.
- Mettre le curseur sur rapide puis cliquer sur 1 dé (engendrer les enfants 1 par 1) ou 2 dés (engendrer toute la génération) pour obtenir la génération suivante, puis recommencer sur minimum 20 générations.
- Noter la fréquence de l’allèle A atteinte au cours des générations la plus éloignée de la fréquence initiale (p = 50%)
- Refaire l’expérience avec les mêmes paramètres plusieurs fois. Noter les fréquences et vos remarques.
- Changer ensuite l’effectif de la population à 50 et recommencer les étapes précédentes.
- Expliquer d’où viennent les différences observées entre les différents essais.
La fréquence de l’allèle ne doit théoriquement pas varier et doit être stable au cours des générations selon le modèle de HW.
- Proposer alors une explication à l’écart constaté entre fréquences observées et fréquences théoriques dans les différentes populations. Quel est le rôle des effectifs ?
En conclusion, à l’aide des 2 cas précédents et du document suivant, lister les 5 conditions nécessaires pour que la structure génétique d’une population soit stable donc en accord avec la loi de Hardy-Weinberg.
Le cas des geais de Floride

La structure génétique d’une population naturelle de geais à gorge blanche (Aphelocoma coerulescens) a été étudiée pendant plus de 20 ans en Floride. Cette population a connu des niveaux élevés d’immigration : les individus immigrant représentent 32 à 55 % des adultes reproducteurs sur une année.
Un individu en se reproduisant avec la population existante, intègre leurs allèles. On parle de flux de gènes.
Évolution des fréquences alléliques d’un SNP suite aux immigrations successives.
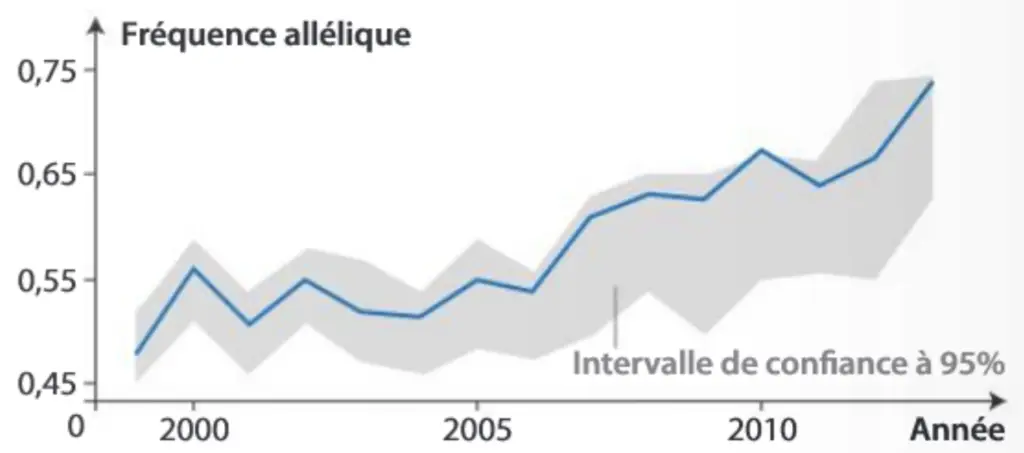
Les SNP (ou Single Nucleotid Polymorphism) sont des séquences d’ADN qui présentent des variations ponctuelles de l’ADN très fréquentes entre individus, à l’origine de nombreux allèles. Leur analyse est riche pour évaluer la diversité génétique d’une population.
DM : Exercice d’application
La mucoviscidose est l’une des maladies héréditaires mortelles les plus répandues en France. Elle est liée à l’allèle récessif d’un gène autosomal qui code pour une protéine transportant les ions chlorures à travers la membrane plasmique.
Un individu sur 2500 est atteint de cette maladie.
On s’intéresse à une famille dans laquelle la maladie a déjà été observée ;
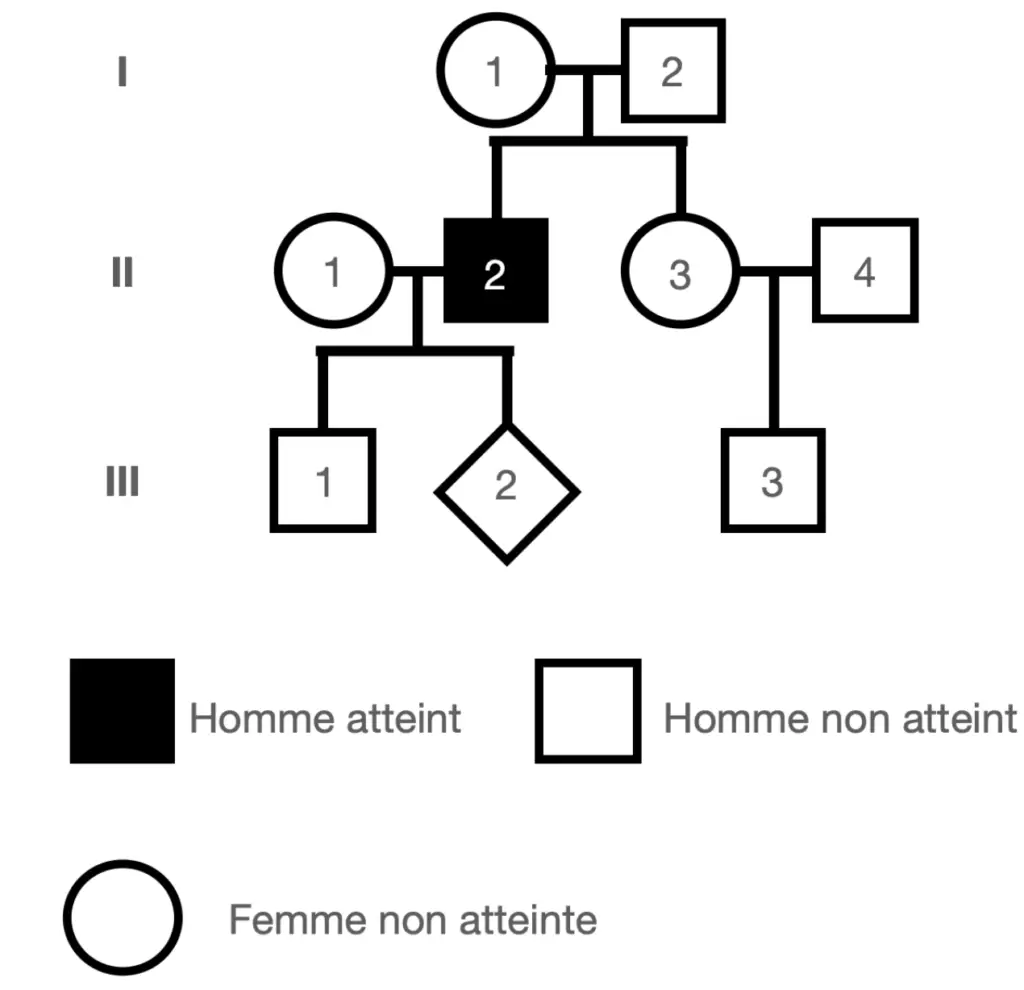
Déterminer le risque statistique pour que l’enfant à naitre III2 soit atteint de cette maladie.
Pour cela utilisez la loi de Hardy Weinberg pour calculer la fréquence des génotypes hétérozygotes (comme celui de la mère de l’enfant), puis calculer le risque pour le fœtus.
Autre exemple d’utilisation de la loi de Hardy Weinberg :

Chez les plants de tomates, l’allèle (m+) qui donne la forme ronde aux tomates domine complètement sur l’allèle (m) qui donne une forme multiloculaire.
Dans une population de 1222 plants de tomates, on trouve que 69 % des individus forment des tomates rondes. On voudrait alors connaître la fréquence de l’allèle dominant et le nombre d’individus homozygotes pour m+ ?

Solution :
69% correspond à l’ensemble des individus [tomates rondes] soit 0,69 pour les individus dominants (Homozygotes et hétérozygotes). On a alors p2 + 2pq. Donc comme p2 + 2pq + q2 =1, on a alors p2 + 2pq = 1 – q2 = 0,69
Donc q2 = 1 – 0,69 <=> q2 = 0,31 <=> q = 0,557
Comme p + q = 1 on a donc 1-q = p soit p = 0,443
L’allèle dominant (m+) a pour fréquence p = 0,443
les homozygotes sont représentés par la valeur p2, soit 0,1849. En multipliant pas le nombre total d’individus on obtient le nombre d’homozygotes (m+//m+) [tomates rondes] qui est de 0,1849 x 1222 = 225,95 tomates, soit en arrondissant à l’entier 226 tomates.
