

Introduction : Beaucoup de méthodes ont été utilisées au fur et à mesure par les scientifiques qui se sont succédés afin de déterminer l’âge de la Terre. Cela a abouti à un rallongement de l’âge de la Terre. Mais il faudra attendre le XXe siècle pour définitivement mettre fin à une controverse vieille de presque 400 ans et permettre à la communauté scientifique d’être d’accord.
Problème : Comment l’approche du calcul de l’âge de la Terre a-t-elle évoluée au XXe siècle ? Comment ont été réalisés les calculs pour aboutir à l’âge de la Terre ?
Objectifs :
Interpréter des documents historiques en lien avec l’âge de la Terre
Connaître et appliquer les méthodes de calcul ou de datation de la Terre
Comprendre l’utilisation des isotopes dans le calcul des âges
Compétences travaillées dans le TP (grille à la fin)


I- Retour sur la salinité des océans et le début du XXe siècle.
1- D’après le document 1 et le document 3, critiquer la méthode employée par Joly pour calculer l’âge de la Terre
Doc. 1 : La logique de John Joly mise à mal


L’âge de la Terre est aujourd’hui bien connu et notablement plus vieux (4.500 Ma) que les idées de Jolly (et de Kelvin) ne le suggéraient… Quelque chose dans les hypothèses de Jolly doit donc être incorrect. Nous allons voir que cette analyse est la clé de la question de la salinité de la mer.
- La masse de l’océan (MO) est considérée comme fixe : la stratigraphie nous indique que le niveau des mers n’a guère varié de plus de quelques centaines de mètres depuis l’Archéen. Cette hypothèse n’est pas donc pas déraisonnable.
- L’apport d’eau des rivières (QR) n’a pas varié. Ceci n’est probablement pas très faux si l’on tient compte de l’hypothèse précédente.
- L’océan ne perd pas de sodium (Na constant), ce que l’on sait être faux puisque du sel évaporitique se forme en diverses régions littorales arides et que cet élément est échangé pour du calcium lors de l’altération sous-marine des basaltes du plancher océanique.
- Jolly suppose également que l’état initial de l’océan est de l’eau douce. Il est donc en train de se « remplir » du sodium libéré par l’altération en milieu continental. Nous découvrons ici un gros problème. Comme il faut 100 Ma pour apporter à l’océan le sodium qu’il contient, celui-ci a forcément du être éliminé (voir point précédent) au fur et à mesure, à la même vitesse. Depuis le début de l’histoire de la Terre, le sodium marin a donc été renouvelé approximativement 4.500 / 100 soit 45 fois. La mémoire de la concentration initiale en sodium est perdue et l’océan a atteint un régime stable (dit état stationnaire).


2- En quoi le document 2 confirme-t-il la critique ? Et qu’a finalement découvert Joly ?
Doc. 2 : Concentrations dans l’eau de mer et les rivières et temps de résidence des éléments les plus concentrés de l’eau de mer.
| | Concentration eau de mer (mmol/kg) | Concentration rivières (mmol/kg) | Temps de résidence t (Ma) |
| Ca2+ | 10,3 | 0,367 | 1 |
| SO4 2- | 28 | 0,12 | 9 |
| K+ | 10,2 | 0,036 | 11 |
| Mg2+ | 53 | 0,15 | 14 |
| Na+ | 470 | 0,315 | 58 |
| Cl– | 550 | 0,23 | 94 |
| Masse de l’océan : MO | 1,41.1021 kg | | |
| Apport d’eau de rivière : QR | 3,6.1016 kg/a | | |
Doc 1 et 2 : D’après https://planet-terre.ens-lyon.fr
Doc. 3 : Mécanismes physicochimiques et biologiques régulant la concentration des composés dissous dans l’eau de mer.
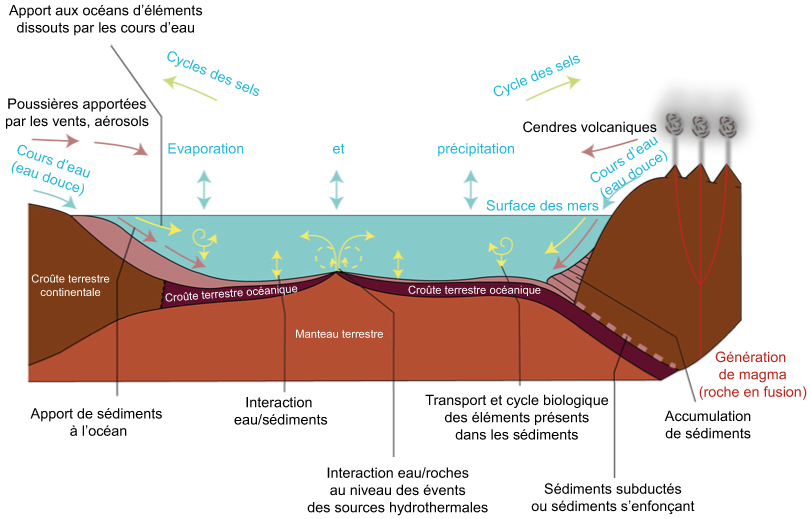

D’après Open University (Cambridge University)
Complément : Une théorie concurrente parfaitement crédible :


un jeune marin breton reçut de sa mère un petit moulin à sel destiné à lui permettre de saler sa soupe lorsqu’il partait en mer. Le problème est que les appareils électroménagers de ce temps-là nécessitaient l’emploi de formules magiques qui tenaient lieu d’interrupteur ON/OFF. Ayant un beau jour oublié le mot magique qui arrêterait le petit moulin et ne voulant pas sombrer avec son bateau qui s’emplissait de sel, le marin dut se résoudre à jeter l’ustensile par dessus bord. Cette théorie est toujours en cours d’expertise…
II- Le calcul de Patterson s’appuie sur la connaissance des isotopes en physique
Détermination de l’âge de la terre par Clair Cameron Patterson


En utilisant des connaissances en physique et les mathématiques, on montre que les rapports de Pb207/Pb204 et Pb206/Pb204 contenus dans des échantillons de même âge sont liés par une relation du type :
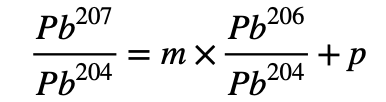
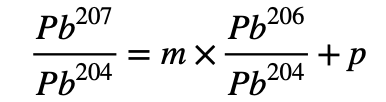
(E)
Clair Patterson mesure alors les rapports Pb207/Pb204 et Pb206/Pb204 dans 5 météorites et dans des sédiments marins.
Doc. 4 : Mesures effectuées par Clair Cameron Patterson.


| Sédiments marins |
| Pb206/Pb204 = 19,00 ; Pb207/Pb204 = 15,80 |
| Météorites | Rapports isotopiques en plomb | ||
| Pb206/Pb204 | Pb207/Pb204 | Pb208/Pb204 | |
| Nuevo Laredo, Mexico | 50,28 | 34,86 | 67,97 |
| Forest city, Iowa | 19,27 | 15,95 | 39,05 |
| Modoc, Kansas | 19,48 | 13,76 | 38,21 |
| Henbury, Australia | 9,55 | 10,38 | 29,54 |
| Canyon Diablo, Arizona | 9,46 | 10,34 | 20,44 |


1- Utiliser un tableur pour représenter le nuage de points de Pb207/Pb204 = f(Pb206/Pb204)


Coup de pouce ?
2- La forme du nuage de points correspond-elle à la relation (E) ?
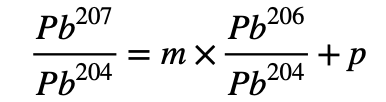
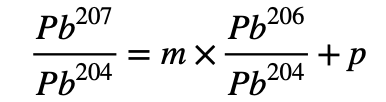
3- Utiliser le tableur pour déterminer une valeur arrondie au dix-millième des réels m et p.


4- L’âge de l’échantillon est lié au nombre m. D’après le doc 5, à quel âge peut-on estimer l’échantillon ?
Doc. 5 : Valeurs m selon l’âge de l’échantillon.
| Age en Ga | Pente de la droite |
| 4,4 | 0,557 |
| 4,41 | 0,561 |
| 4,42 | 0,565 |
| 4,43 | 0,569 |
| 4,44 | 0,573 |
| 4,45 | 0,577 |
| 4,46 | 0,581 |
| 4,47 | 0,585 |
| 4,48 | 0,589 |
| 4,49 | 0,593 |
| 4,5 | 0,597 |
| 4,51 | 0,601 |
| 4,52 | 0,605 |
| 4,53 | 0,609 |
| 4,54 | 0,613 |
| 4,55 | 0,618 |
| 4,56 | 0,622 |
| 4,57 | 0,626 |
| 4,58 | 0,631 |
| 4,59 | 0,635 |
5- Pourquoi ceci constitue aussi une estimation de l’âge de la terre ?


